この記事では「モンテカルロシミュレーション」について説明しています。
言葉自体を聞いたこともない！という方から
聞いたことあるけどイマイチ理解できない…という方まで
ぜひ、参考にしてくださいね。
あーぁ、未来が読めたらなぁ。
どうしたの？
未来は何が起こるか分からないし
不確定すぎて
どうしたら良いのか
分からなくなっちゃうよ…。
確かに、未来を予測することは
不可能だけど
計算によってシミュレーションはできるよ！
そんな方法があるの！？
知りたいな！
潜在的な結果を予測することで
円滑に進められたり
リスクヘッジもできるよ。
モンテカルロシミュレーションは、
不確実な事象について起こり得る結果を予測する手法です。
不確実性の高い現代の市場環境では
非常に役立つ分析と言えるでしょう。
ビジネスにおいて、
どのようなリスクが考えられるのか？
危険性や発生確率はどのレベルなのか？
といったことを計算によって導き出します。
未来を予測することは不可能ですが、
潜在的な結果をあらかじめ予測しておくことで、
意思決定をスムーズに進めるだけでなく、
リスクから受ける影響も軽減することができます。
この記事では、
モンテカルロシミュレーションについて概要からメリット、活用例まで
解説していますのでご活用ください。
【モンテカルロシミュレーションとは】
▶︎モンテカルロシミュレーション
ビジネスにおいても他場面においても
何かの決断をするとリスクの可能性も必ずついてきます。
未来を予測することは不可能ですが
ランダムな試行を繰り返し、計算することによって
リスクも含めた潜在的な結果を導き出すことができます。
モンテカルロ・シミュレーションは
このように不確実な事象に対して、起こり得る結果を予測できる
分析手法の１つです。
▶︎モンテカルロシミュレーションの仕組み
不確かなことが起こる確率を計算する方法です。
- 複数のモデルを作成する
- 乱数を使用する
- それぞれのモデルに乱数を代入して計算する
- 何千回も何万回も計算を繰り返す
- さまざまな結果がどのくらいの確率で起こるかを予測する
後述していますので、ぜひ参考にしてください。
モンテカルロシミュレーション
難しそうだ…
と思ったら、外注も１つの手！
▶︎一般的な確率分布
モンテカルロシミュレーションを使うと、いろいろな結果がどのくらいの確率で起こるかを示す分布を得ることができます。これから、よく使われる確率分布について簡単に説明します。
正規分布
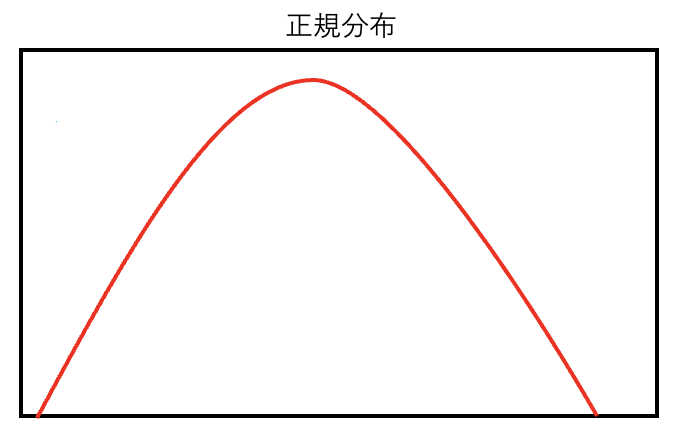
真ん中が高くて両側が低い山のような「釣鐘曲線」という形をしています。
この形の分布では、真ん中の値、つまり平均値の周りの数が一番多く出ることが多いです。
対数正規分布
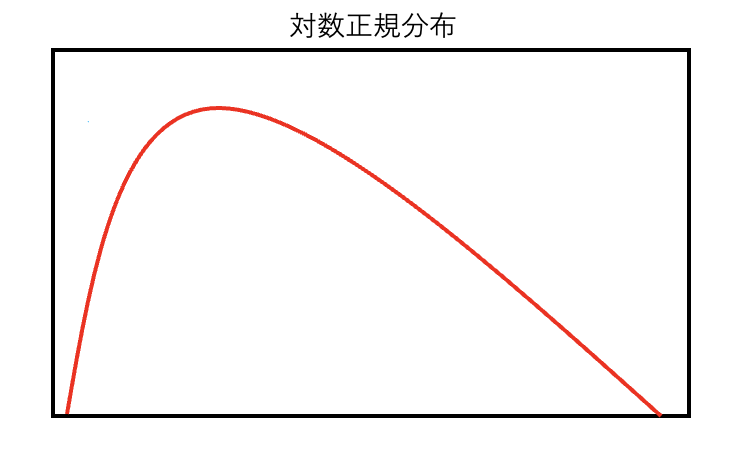
左右対称ではなく、右側に長く伸びた形の曲線です。
この分布では、値がゼロより大きく、右側に向かって伸びていきます。
三角分布
三角形のような形をした確率分布です。
この分布では、
- 【最小値】一番小さい値
- 【最尤値】一番ありそうな値（最ももっともらしい値）
- 【最大値】一番大きい値
の範囲をユーザーが決めます。
一様分布
長方形の形をした確率分布で、
この分布では、すべての結果が起こる確率が同じです。
PERT分布
PERT分布は
- 【最小値】一番小さい値
- 【最尤値】一番ありそうな値（最ももっともらしい値）
- 【最大値】一番大きい値
がある点で三角分布に似ています。
この分布では、一番ありそうな値の近くの数が出る確率が高くなります。
そして、三角分布よりもなめらかな形をしています。
離散分布
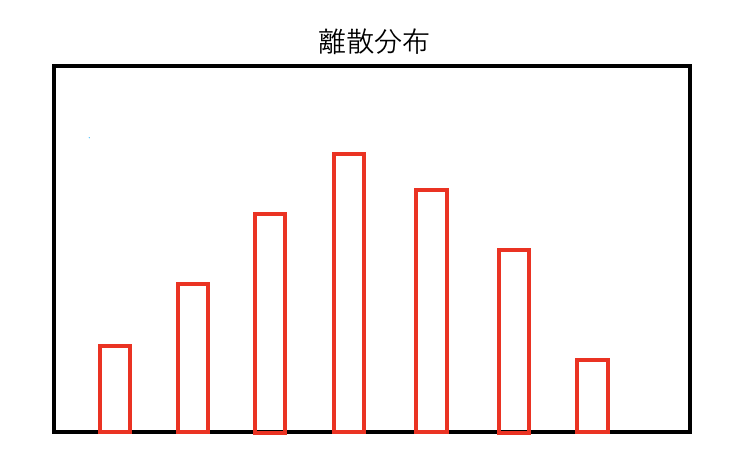
離散分布では、起こり得る値それぞれが
どれくらい起こりやすいか（尤度）が定義されます。
さまざまな結果やそれが起こる確率を
詳しく広く理解することができます。
これは、起こり得る結果や分布が多様だからです。
確率分布も難しいし、自分でできなさそう…と思ったら
▶︎モンテカルロシミュレーションのメリット
モンテカルロシミュレーションは
下記のメリットがあります。
- 様々な値を使って計算でき、多角的に見ることができる。
. - ただの予測よりも、よりはっきりとした状況を示すことができる。
. - コストやスケジュールを現実に合わせて設定や修正ができる。
. - 将来のリスクを数値で示して、どんな問題が起きるか予測できる。
. - 確率分布をグラフで見せられるから、結果が分かりやすい。
. - どんな結果がどれくらいの確率で起こるかを示せる。
. - どの変数が結果にどう影響するか、どの入力でどんな結果が出たかを調べられる。
【モンテカルロシミュレーションのやり方】
▶︎（01）乱数発生
モンテカルロシミュレーションの核となるのは、
いろんな確率で起こる事をランダムな数値を使って何度も試してみることです。
最初の試行結果が次の試行に影響しないように乱数を使います。これにより、様々な条件を詳しく計算できるのです。
▶︎（02）将来予測
このステップでは、乱数を使って、未来に起こりうるたくさんのシナリオを計算します。
結果は多数の試行用数値を統計で分析することで得られ、サンプルがたくさんあればあるほど、結果は正確になります。
▶︎（03）結果推定
最後のステップは、たくさんのシナリオについて計算し、その平均を出します。十分な量のシミュレーションをすることで、信頼できる指標が得られるのです。
ちょっと難しそう…
と思ったら
▶︎Excelでモンテカルロシミュレーションを試す
Excelで
モンテカルロシミュレーションに
チャレンジ！
例題
・海賊に対する海軍の攻撃は70%の確率で命中
・ダメージは60～69の間の整数値を取る
海賊のHPが65である場合、
海軍が海賊に勝つ確率（HPを0以下にできる確率）は何％か？
計算上の確率は…
勝つために65〜69のダメージを出す確率 50%
↓ ↓ ↓
70％×50％が勝つ確率＝35%
（01）命中判定を出す
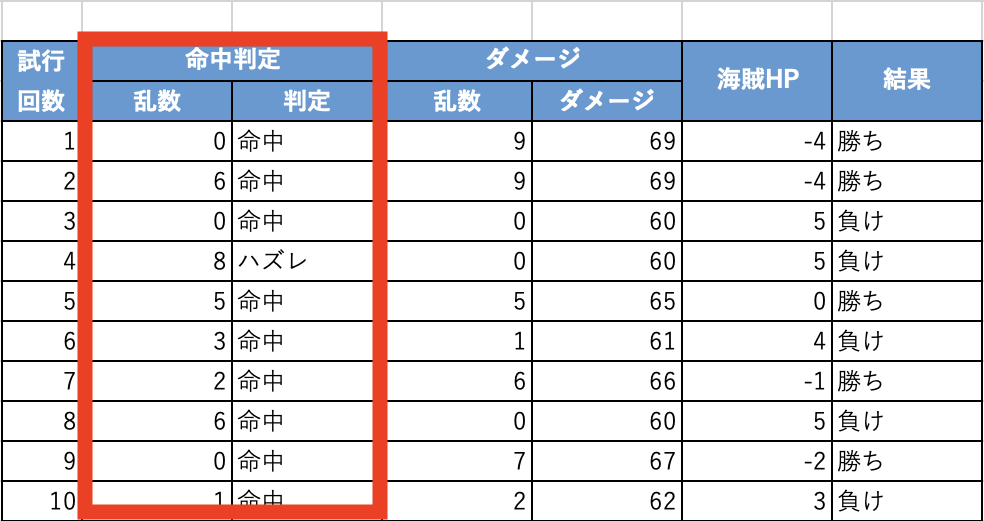
【乱数列】
- RAND関数で乱数（0〜１未満）を生成する
- 乱数に10を掛け算し、INT関数で0~9の整数を取るようにする
【判定列】
- 7より小さい数（0〜7）が出る確率が70%
- ７より小さかったら「命中」、それ以外は「ハズレ」
（02）ダメージ数を出す
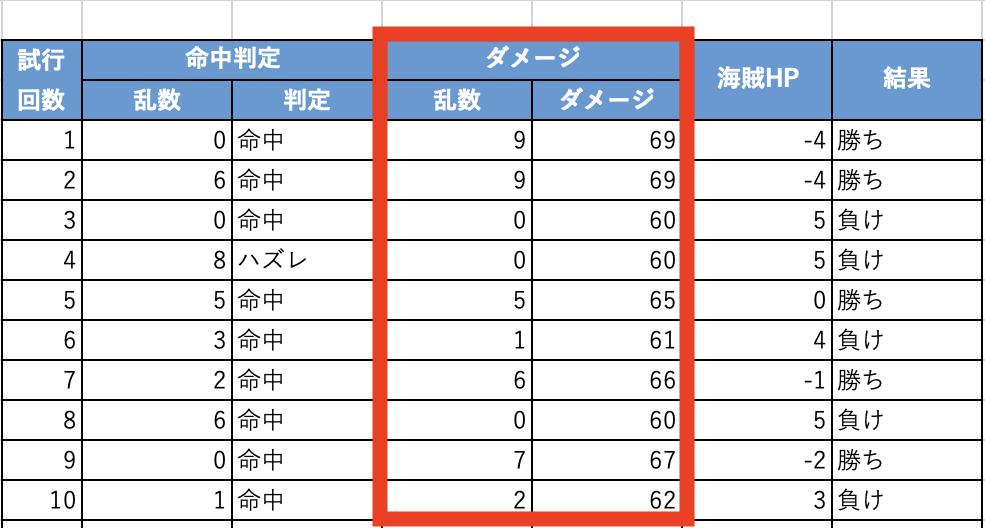
【乱数列】
- ＜命中の場合＞
RAND関数で乱数（0〜１未満）を生成する
乱数に10を掛け算し、INT関数で0~9の整数を取るようにする - ＜ハズレの場合＞
乱数列は0に設定
【ダメージ列】
- ダメージは60~69の整数なので、乱数（0〜9）＋60で計算
（03）攻撃後の海賊のHPを出す
- 攻撃前の海賊HP65からダメージ数を差し引く
（04）勝負判定を出す
- 海賊HPが０以下：勝ち
- 海賊HPが０より大きい：負け
（05）勝つ確率を出す
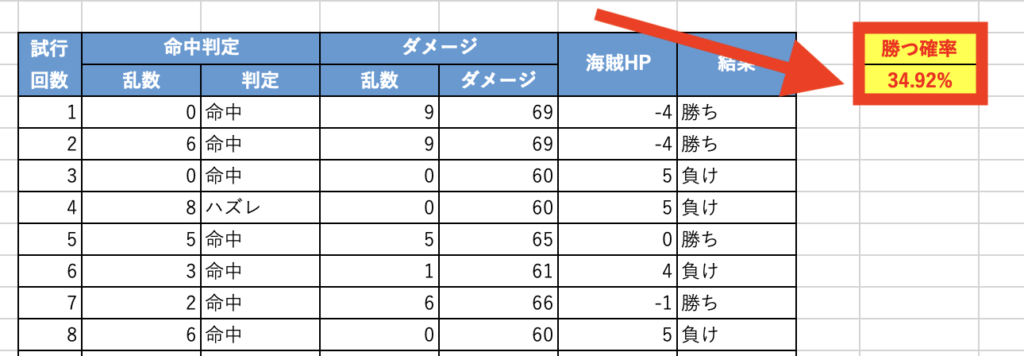
- 「勝ち」の数をカウント
- 「勝ち」の数を全試行回数で割る
.
（結果）シミュレーション結果
今回は、試行回数5000回でやってみました！
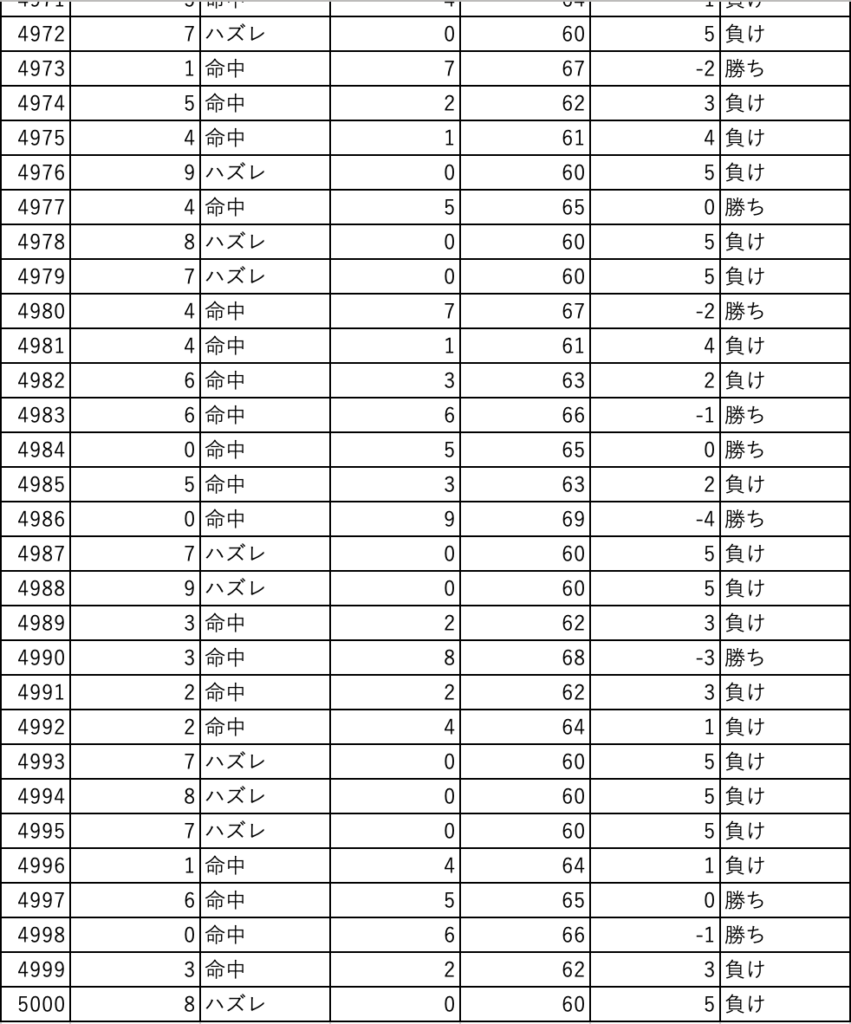
結果は、34.92％！
理論上は35％ですが、かなり近い結果が得られました。
今回の試行は5000回なので、誤差が出ていますが
試行回数を増やしていけば精度が高まることが予想されます。
＼すごいけど、自分にはできない…/
【モンテカルロシミュレーションの活用例】
▶︎ビジネス
- プロジェクト管理
- 企業が陥るリスクを評価する
- 為替や株価の変動をシミュレーションする
▶︎学問
- 天文学
- 気象学
- 素粒子物理学
▶︎オンラインゲーム
- ゲームバランスをシミュレーションする
▶︎エンジニアリング
- 耐久性の推定
- 信頼性と堅牢性の確保
【モンテカルロシミュレーションまとめ】
▶︎▶︎モンテカルロシミュレーション◀︎◀︎
不確かなことが起こる確率を計算する方法です。
-
- 複数のモデルを作成する
- 乱数を使用する
- それぞれのモデルに乱数を代入して計算する
- 何千回も何万回も計算を繰り返す
- さまざまな結果がどのくらいの確率で起こるかを予測する
モンテカルロシミュレーション
どうだった？？
計算で予測ができるなんて
すごい手法だね。
多角的に考えられるのもイイ！
そうだよね。
何をするのでもリスクを考えるのは
大事なことだから、役立ててね。
ここまでモンテカルロシミュレーションを
説明してきましたが
いかがでしたか？？
使ってみよう！という方は、ぜひご活用くださいね。
ちょっと難しいかも…と思った方も大丈夫！
私たちは、そういった相談も受けているので
まずはお気軽にお問い合わせください。
